Tre punti di vista sulle cose: le proiezioni ortogonali

Dall’alto, di fronte, di lato.
Bastano questi tre punti di vista per descrivere visivamente qualsiasi oggetto. Tre viste (ma a volte ne bastano due, a volte ne servono quattro) che costituiscono le proiezioni ortogonali, o metodo di Monge.

Sono considerate una rappresentazione oggettiva, fedele. Ma in realtà nessuno di quei punti di vista è possibile per l’occhio umano, perché presuppone una distanza infinita dall’oggetto osservato, tale che questo non subisca deformazioni prospettiche.

Quando, infatti, guardiamo un oggetto a distanza ravvicinata, le linee tra loro parallele appaiono convergenti. Via via che allontaniamo l’oggetto, queste linee convergono sempre meno. Se riuscissimo ad allontanarci fino a un punto posto all’infinito (ma con uno zoom potentissimo…), le linee parallele tornerebbero ad essere tali.

Dunque le proiezioni ortogonali sono quanto di più astratto e cerebrale abbia partorito la mente umana. Nonostante ciò, le prime rappresentazioni di oggetti fatte dall’uomo, presuppongono proprio questa impostazione tutta mentale piuttosto che visiva. Mi vengono in mente i famosi giardini egizi: vasche d’acqua viste in pianta; alberi, barche ed edifici rappresentati in alzato o in sezione.

Certo non si trattava di una rappresentazione a scopo tecnico (cioè restituire dimensioni e forma esatta degli oggetti) ma dell’unico modo che avevano gli Egizi di raffigurare spazi e cose senza la simulazione della terza dimensione.
Quello scopo pratico e informativo si ritrova invece con i Romani: la famosa Forma Urbis Romae, la planimetria della città incisa su marmo risalente all’inizio del III secolo d.C., è una gigantesca proiezione orizzontale del piano terra di tutti gli edifici, pubblici e privati. Una mappa catastale ante litteram.

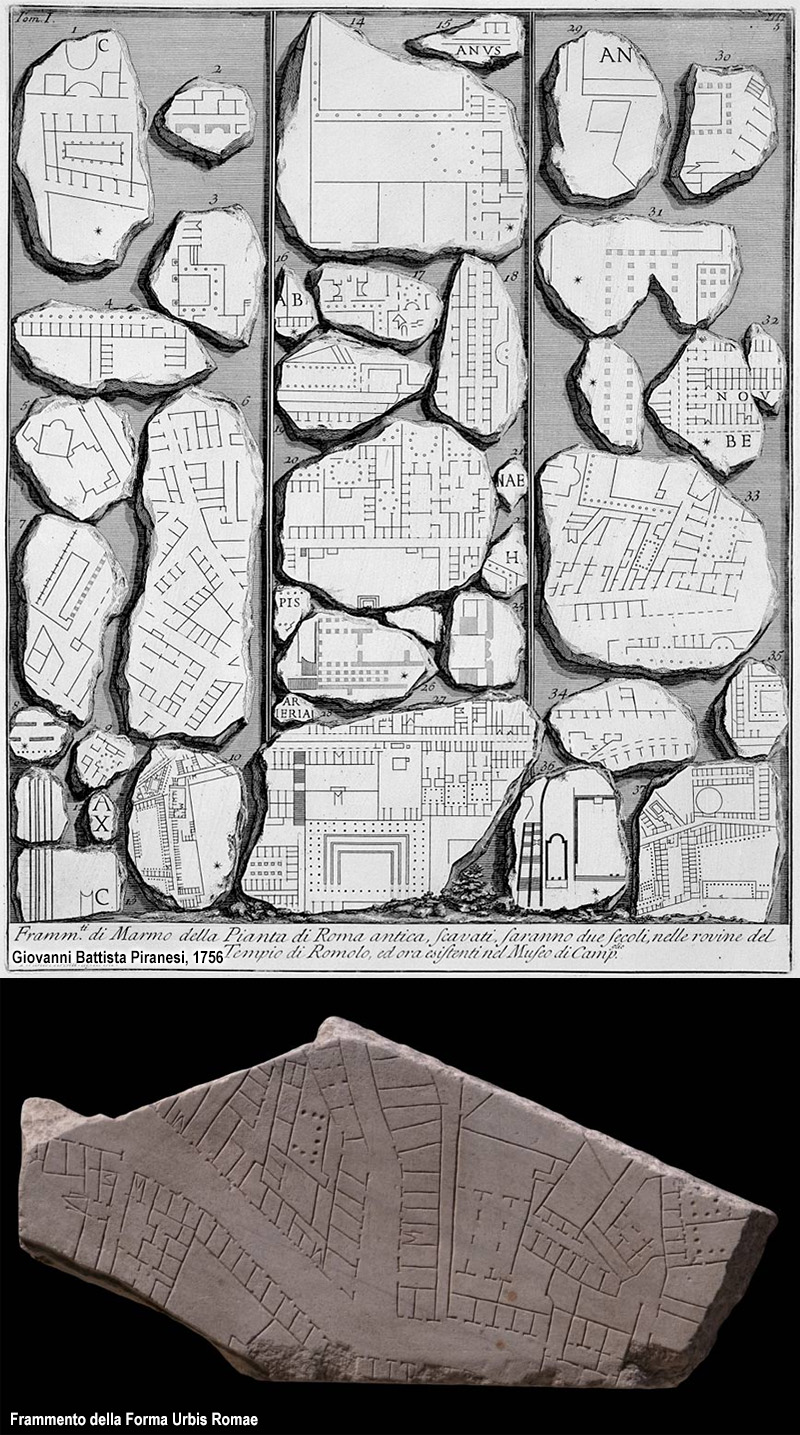
È un punto di vista astratto. Una rappresentazione ‘matematica’ dello spazio. Ma manca ancora la correlazione con le viste in alzato, vera peculiarità delle proiezioni ortogonali.

Nulla di nuovo durante il Medioevo: nei suoi celebri taccuini l’architetto Villard de Honnecourt (XIII sec.) raffigura con cura piante e alzati di chiese gotiche (particolari del coro o degli archi rampanti), mostrando grande intuito per la rappresentazione tecnica. Ma ancora si tratta di viste separate.

È con il tardo Rinascimento che compaiono i primi disegni (sia progetti di nuovi edifici che rilievi di architetture esistenti) nei quali si può osservare una corrispondenza precisa tra pianta e alzato. L’approccio razionale alla rappresentazione tipico di quest’epoca, che già si era manifestato con la codifica della prospettiva, non poteva che portare alla ricerca di una forma di disegno della realtà il più possibile oggettivo.

Gli esempi più noti sono quelli di Palladio, soprattutto i rilievi di architetture romane, misurate e rappresentate per carpirne ogni segreto. In questi si può notare il prospetto in alto e la pianta (sezionata e campita) in basso.

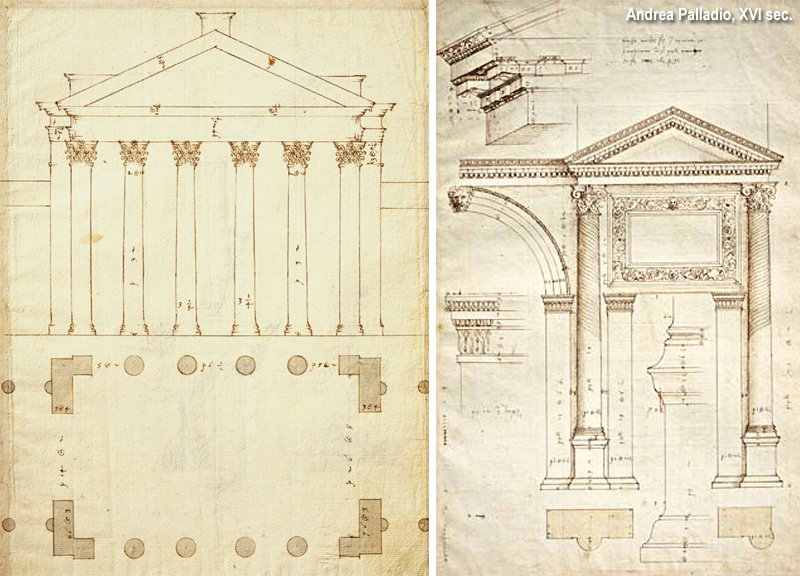
Ci vuole un’altra epoca di grande fede nella ragione per arrivare alla descrizione definitiva del metodo delle proiezioni ortogonali: siamo in pieno Illuminismo quando il francese Gaspard Monge (1746-1818), matematico e disegnatore, elabora la sua Geometria descrittiva (1794), cioè la disciplina che si occupa della rappresentazione di oggetti attraverso operazioni di proiezione sul piano.
La definizione sembra un po’ complicata ma in effetti le proiezioni ortogonali si chiamano così proprio perché si immagina di proiettare, come fosse un’ ombra, la forma dell’oggetto su un piano retrostante.
Il termine ortogonale deriva invece dal fatto che la direzione di proiezione è ortogonale (cioè perpendicolare) al piano.
Proiettando l’oggetto da tre direzioni sui piani del triedro (i tre piani ad angolo retto tra loro) e ribaltando il piano verticale (PV) e quello laterale (PL) sullo spesso piano di quello orizzontale (PO) si ottiene il tipico disegno diviso in quattro parti con le tre viste dello stesso oggetto.

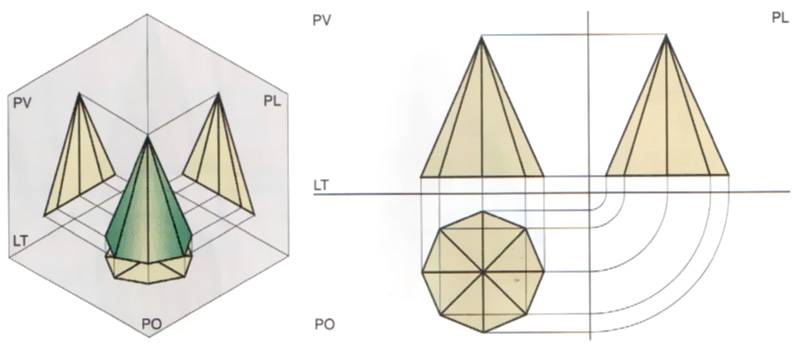
Sembra facile, detto così. Quando guardiamo un oggetto rappresentato in proiezioni ortogonali si capisce anche intuitivamente come funzionano. Sia che si tratti di tre viste che di due.

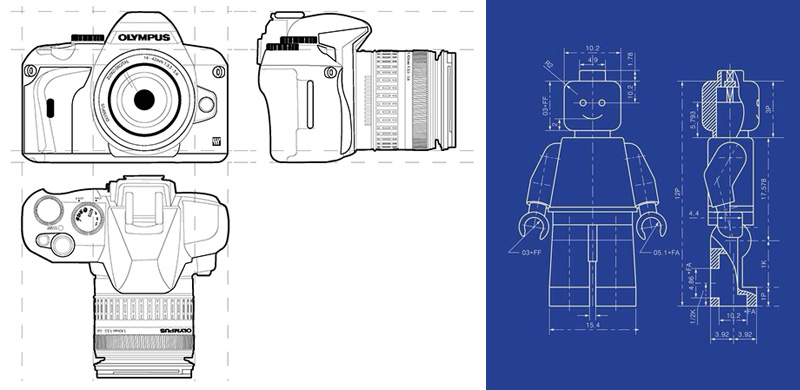
Non ci vuole molto, insomma, a ricostruire mentalmente l’oggetto tridimensionale da cui provengono.

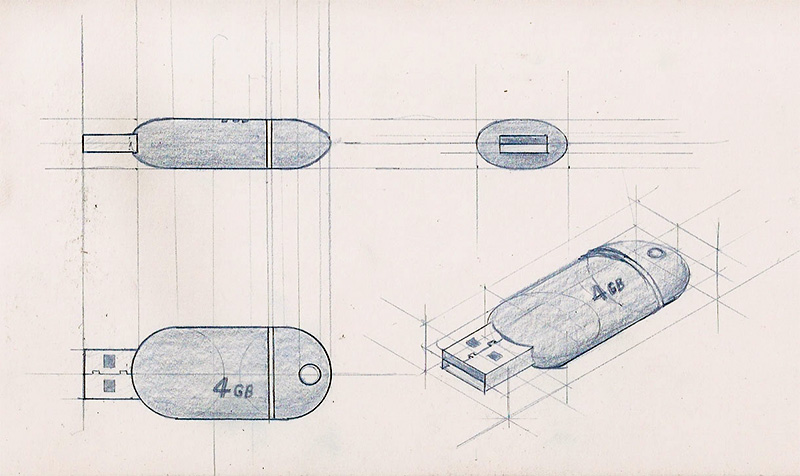
Ma appena si tratta di disegnarle tutto diventa più complicato, specie se si parte da un oggetto rappresentato in assonometria.
Per questo motivo l’anno scorso ho sperimentato in classe le proiezioni ortogonali basate sull’osservazione delle costruzioni di legno. Un esercizio che ha notevolmente semplificato l’impatto con un tipo di rappresentazione tanto astratto, rendendolo concreto e maneggevole.

Quest’anno, invece, ho provato con un percorso fotografico testandolo per la prima volta con gli studenti della collega Francesca Santeusanio, al liceo scientifico Galilei di Pescara: con il cellulare si doveva fotografare un oggetto qualsiasi, di piccole dimensioni, dai tre punti di vista canonici e montare le tre immagini secondo lo schema delle proiezioni di Monge usando un’app per fare presentazioni o collage fotografici.
Per cominciare ne ho fatto uno io, usando un mouse come soggetto.

Dopo è stato il loro turno. In coppia hanno scelto l’oggetto (persino le loro stesse scarpe) e lo hanno fotografato.

Successivamente hanno montato le tre viste come richiesto.

Infine mi hanno inviato il file in modo da poterlo visionare sulla LIM e discuterne insieme.

Abbiamo così notato in alcuni casi la mancata corrispondenza delle dimensioni nelle tre proiezioni, o l’asse di visione non perfettamente perpendicolare al piano di proiezione oppure una distanza troppo ravvicinata che ha distorto le forme o anche un errore nel posizionamento delle tre viste sui tre quadranti.

Ho riproposto l’esercizio anche ai miei studenti. Conoscendo già gli errori tipici fatti dai ragazzi di Pescara ho segnalato gli aspetti da considerare con attenzione.

E alla fine sono rimasta molto soddisfatta dal risultato:  abbiamo raggiunto una consapevolezza maggiore su un processo molto astratto, abbiamo usato in modo utile il cellulare e ci siamo preparati bene alle successive lezioni di disegno con squadrette e matita avendo chiaro il senso delle linee che andremo a tracciare.

Sicuramente da ripetere.

 

SalvaSalva

SalvaSalva

SalvaSalva