Geometria e arte: la simmetria radiale

Mi ha sempre affascinato tutto ciò che è circolare. E tra tutto ciò che è circolare mi attraggono particolarmente tutte quelle figure che mostrano delle simmetrie radiali, dei disegni simmetrici rispetto a tre, quattro, cinque, sei o più raggi.

Gli esempi più noti ci vengono dalla natura: cosa sono i fiocchi di neve se non delle costruzioni straordinarie a simmetria radiale?

Proprio con i fiocchi di neve si possono realizzare interessanti esercizi grafici per imparare a disegnare oggetti a simmetria radiale.

Molti organismi viventi, tra flora e fauna, presentano simmetrie radiali. Basta guardarsi intorno: quanti assi di simmetria hanno un fiore, la sezione di un frutto, una stella marina, o un riccio di mare?

In questo caso può essere utile, dal punto didattico, far fare agli studenti una raccolta fotografica di elementi con simmetria radiale che scorgono intorno a loro.

Oppure si possono ammirare, in contemplazione estatica, le bellissime tavole tratte da “Forme artistiche della natura” dello scienziato Ernst Haeckel.

L’uomo ha preso spunto dagli organismi a simmetria radiale fin dai tempi più antichi. All’epoca romana risalgono alcuni esempi di pavimenti musivi con geometrie raggiate particolarmente complesse come negli esempi sottostanti di Saragozza e Leptis Magna.

Tuttavia uno dei momenti di massimo splendore delle simmetrie radiali si deve all’arte araba. Il divieto di rappresentare figure sacre ha portato la cultura figurativa islamica ad orientarsi verso i pattern geometrici con esempi in opus sectile dagli incredibili intrecci.

Anche questa forma artistica si presta bene all’esercitazione grafica degli studenti. Prendendo come spunto un pattern geometrico piuttosto semplice come la stella ad otto punte, se ne può fare il ridisegno cercando di comprenderne le simmetrie fondamentali e i poligoni di base.

Un altro esempio relativo alle cosiddette “arti minori” è costituito dalle fibule medievali, gioielli in oro e smalti realizzati dai Franchi e dai Longobardi con decori geometrici basati generalmente su due assi di simmetria.

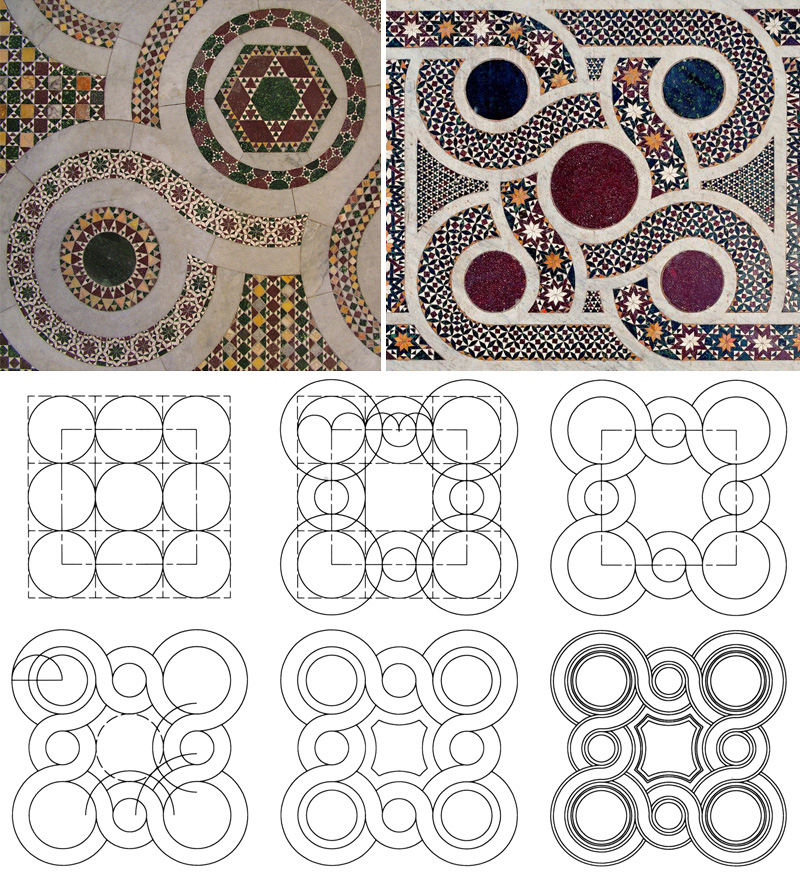
A partire dal basso Medioevo si può osservare un’altra manifestazione artistica legata alle simmetrie radiali: i pavimenti cosmateschi. Si tratta di distese marmoree in opus sectile con intrecci basati su geometrie di cerchi e quadrati presenti in tantissime chiese italiane.

Sempre al basso Medioevo appartengono i rosoni, esempi “da manuale” di simmetria radiale, vere e proprie opere d’arte cariche di simboli e di affascinante bellezza.

La geometria del rosone si presta bene allo studio grafico e al ridisegno da parte degli studenti. Si può cominciare con un semplice rosone romanico per proseguire con esempi più complessi tipici dell’arte gotica.

Nelle manifestazioni artistiche contemporanee si continuano a trovare eccezionali esempi di simmetrie radiali composti da qualsiasi materiale e su qualsiasi supporto.

Simili a vetrate gotiche sono le grandissime composizioni di ali di farfalla di Damien Hirst. Al di là delle polemiche sull’artista che le ha create e sull’uso di parti di animali, si tratta di lavori molto interessanti dal punto di vista delle complesse geometrie sottese.

L’effetto ricorda molto le sfaccettature visibili nel buon vecchio caleidoscopio, un oggetto che merita di essere mostrato agli studenti (di qualsiasi età) e magari anche creato con le proprie mani. Una versione digitale del caleidoscopio consente di disegnare delle immagini casuali ed osservare come queste diventino simmetriche se osservate da un caleidoscopio virtuale.

Alcuni artisti, come Allison Trentelman, si sono ispirati proprio a questi effetti per elaborare alcune immagini caleidoscopiche partendo da foto di alberi ed altri soggetti naturali.

Quest’artista ha denominato le sue opere “Mandala“. In realtà i mandala sono qualcosa di ben diverso: sono disegni con geometrie raggiate basate sul cerchio e sul quadrato con funzione rituale e spirituale, utilizzati dal Buddhismo e dall’Hinduismo.

Una variante dei Mandala sono i kolam, disegni fatti davanti all’ingresso di casa dalle donne indiane con funzione benaugurale.

 

Sia i mandala che i kolam possono essere disegnati partendo da incroci di cerchi e quadrati e poi colorati liberamente. È un esercizio molto adatto ai più piccoli che possono avere, così, un primo approccio con la geometria e l’armonia di forme e colori che prescinda dalla rappresentazione figurativa.

Sempre per i bambini può essere divertente ed istruttivo l’uso dello spirografo, un kit di rotelline dentate nelle quali fare scorrere le penne per ottenere splendidi disegni con geometrie radiali. Ne esistono anche versioni da realizzare online sebbene, in questi casi, si perda l’esercizio di coordinazione mano-cervello che l’uso di uno spirografo manuale consente.

Occorre sottolineare, comunque, che le figure ottenute con lo spirografo non sono dei semplici disegnini bensì strutture che seguono delle precise formule matematiche. Dunque, in qualche modo, sono adatte anche a studenti delle scuole superiori.

Volendo, invece, lavorare a mano libera, senza l’aiuto delle rotelline, si possono realizzare gli zendala, geometrie centrali simili ai mandala riempite con texture definite zentangle.

Ancora più d’effetto sono gli zendala dipinti sui sassi come quelli di Maria Mercedes Trujillo o quelli di Elspeth McLean.

Alcuni lettori del blog mi hanno suggerito esempi di simmetria radiale ai quali non avevo pensato. I famosi centrini all’uncinetto che altro sono se non mirabili esempi inconsapevoli di geometrie stellari?

L’artista polacca NeSpoon li realizza addirittura a scala urbana.

E che dire dei misteriosi cerchi nel grano? Qualunque origine abbiano, molti esemplari mostrano splendide simmetrie radiali!

A questo punto credo che il limite sia solo la fantasia: provate anche voi a creare delle geometrie stellari utilizzando tutto ciò che trovate in giro. Il risultato sarà senz’altro sorprendente!

Ecco qualche esempio a cui ispirarsi…

… ed ecco quelli che abbiamo fatto in classe. La lezione è servita!

SalvaSalva