Geometria e arte: il triangolo
Uno degli aspetti dell’arte che mi affascina di più è la sua estrema interdisciplinarietà: la produzione artistica è, infatti, strettamente correlata alla storia, alla matematica, alla letteratura, alla geometria, alla musica, alla percezione visiva, alla sociologia, alla chimica, alla psicologia… insomma, non c’è campo del sapere umano che non possa essere collegato all’arte.

Tra queste interrelazioni quella che trovo più sorprendente riguarda il legame indissolubile tra arte e scienza, tra pensiero estetico e logica matematica. Sembrano due mondi inconciliabili, invece è proprio l’arte l’anello di congiunzione!
Si potrebbe pensare, addirittura, di sfruttare l’arte per avvicinare gli studenti alla geometria e alla matematica pensando dei percorsi appositi. In questo post, molto semplicemente, mi interessa evidenziare i legami tra il mondo dell’arte e dell’architettura e quello della geometria partendo dalla più semplice (semplice solo per numero di lati…) dalle figure geometriche piane: il triangolo.
Figura di origine antichissima, appare sotto forma di struttura triangolare nelle antiche immagini della triskeles, simbolo solare dei culti celtici e mediterranei.

Il triangolo appare nella sua forma completa nelle decorazioni, definite “a dente di lupo“, della ceramica del periodo geometrico dell’arte greca.

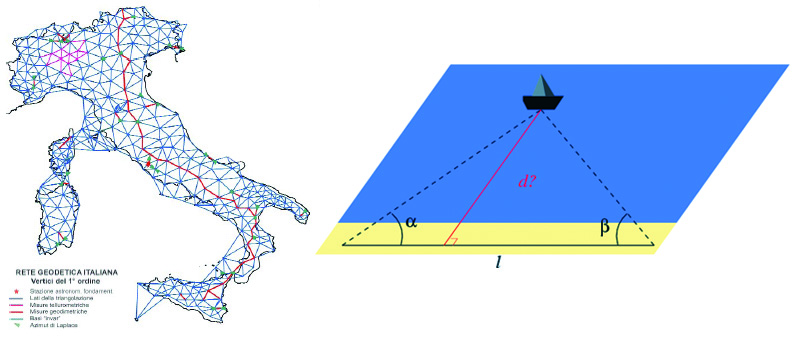
Intanto erano già stati individuati dei triangoli con delle proprietà particolari: il triangolo equilatero (adatto a creare delle maglie regolari), quello rettangolo (i cui lati avevano dei particolari rapporti numerici tali da poter essere calcolati con il teorema di Pitagora o con calcoli trigonometrici) e il triangolo aureo (triangolo isoscele nel quale base e lati sono in rapporto aureo). La triangolazione divenne presto un sistema per rilevare e ridisegnare il territorio.
In epoca cristiana passò rapidamente a simboleggiare Dio e la Trinità. Dalle pale d’altare medievali fino a quelle del Cinquecento è possibile notare talvolta un triangolo dietro la testa di Dio, o sospeso con un occhio onniscente al suo interno.

In epoca gotica il triangolo divenne anche il modulo costruttivo delle facciate delle grandi cattedrali, spesso associato a simbologie esoteriche.

Il triangolo come elemento per l’organizzazione della composizione si ritrova anche nei dipinti del Rinascimento. Qui è possibile notare una disposizione triangolare dei personaggi che conferisce stabilità ed ordine alla scena e che viene ampiamente utilizzata da tutti gli artisti dell’epoca (ma anche oltre).

Intanto, nell’arte islamica, il triangolo era diventato la base di numerosi pattern geometrici.

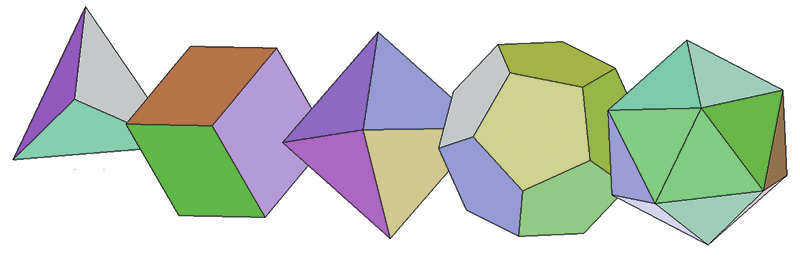
Il triangolo equilatero è anche l’elemento di base di tre dei cinque solidi platonici: il tetraedro (formato da 4 triangoli), l’ottaedro (otto triangoli) e l’icosaedro (20 triangoli).
Appare finalmente più visibile come triangolo in sè, in molte opere astratte di Kandinsky. Per l’artista, d’altra parte, il triangolo aveva significati molto speciali; di questa figura geometrica scrisse: “Un grande triangolo acuto diviso in sezioni uguali, con la parte più piccola e acuta rivolta in alto: così si prospetta giustamente e in modo schematico la vita spirituale… L’intero triangolo si muove lentamente, quasi invisibilmente, con moto progressivo e ascendente, e dove oggi era il vertice si trova domani la prima sezione…”.
Kandinsky associava anche forme e colori e, secondo lui, “I colori pungenti risuonano meglio nella loro qualità quando sono dati in forme acute per esempio il giallo in un triangolo“.

Altro genere sono i triangoli utilizzati da M. C. Escher nelle sue celebri incisioni. Molti dei suoi lavori, infatti, si basano sul cosiddetto “triangolo di Penrose“, una figura geometrica impossibile che nei disegni di Escher crea uno spazio polidimensionale, anch’esso fisicamente impossibile.

Tornando a poligoni più reali, occorre ricordare come il triangolo sia l’unica figura geometrica indeformabile: se i vertici fossero snodi il triangolo non cambierebbe la sua forma mentre il quadrato potrebbe deformarsi e diventare un rombo, un rettangolo tramutarsi in un parallelogramma. Questo ne consente un uso in architettura come elemento di irrigidimento per le cosiddette “travi reticolari” o come modulo per coperture e cupole geodetiche.

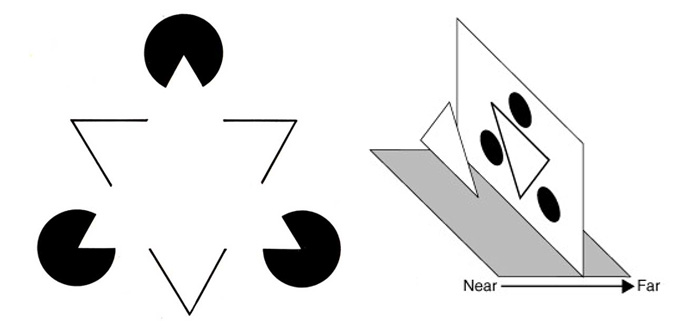
Il triangolo ha una tale forza visiva che riusciamo a vederlo anche quando non c’è come dimostra la famosa illustrazione del triangolo di Kanizsa. In questa immagine si vedono addirittura due triangoli sovrapposti a causa della nostra innata tendenza a completare immagini interrotte secondo la loro forma più semplice e a posizionare sullo sfondo ciò che sembra essere attraversato da qualcos’altro.
Al di là delle proprietà geometriche e ottiche, il triangolo ha un suo fascino al quale non sono immuni neanche gli artisti contemporanei. Guardate questo fantastico poster composto da Storm Thorgerson per il 30° anniversario dell’album The dark side of the Moon dei Pink Floyd… un vero inno al triangolo!
Per finire un po’ di allegria con i bellissimi murales di Matt Moore. Il soggetto? Triangoli, naturalmente!








Ma che meraviglioso spunto per parlare della mateMAGICA come la chiamo io ai miei bimbi. Grazie
😀
Comunque ci rifletto. Chissà.
Bene! Mi farebbe piacere in entrambi i casi. Parlarne o leggerne.
Troppo gentile! Tu mi hai dato voce per riflessioni che tra l’altro non sono il primo a evidenziare. La bellezza è associarle all’arte. Per questo sono io a ringraziare te, visto che come te adoro le letture trasversali. Il prezzo che si paga è un minimo di approssimazione, soprattutto per ciò che attiene la Scienza, nonostante l’ideale di Esattezza di Calvino che condividiamo. Tu ad esempio riesci ad essere esatta senza perdere mai di vista la sintesi. Il tutto con un pizzico di sense of humour e leggerezza. Sono sicuro che prima o poi avremo occasione di parlarne di persona. Sarà interessante e stimolante.
Grazie a te
Senti Gianfranco, ma tu non hai mai scritto articoli con queste tue riflessioni?
Dovresti farci un blog!
Emanuela, mi avventuro qualche passo nella matematica: la tua introduzione è un “assist” irresistibile… ci vado a nozze.
Esistono i numeri triangolari:
1,3,6,10,15,21,28…
Perché triangolari? Meglio guardare la figura seguente: https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/First_six_triangular_numbers.svg/374px-First_six_triangular_numbers.svg.png
In pratica formano di volta in volta un triangolo equilatero il cui lato è costituito da 1, 2, 3, 4 , 5 interi e così via.
Ogni numero triangolare si ottiene sommando i primi n numeri naturali, come si evince dalla figura linkata.
Bene! Superata la parte noiosa, avremo un aneddoto e una magia.
L’aneddoto riguarda il grande matematico tedesco Gauss, vissuto a cavallo della fine del 1700. Si dice che da ragazzino per punizione (immagino un severissimo istitutore prussiano) gli fu assegnato il compito di calcolare la somma dei primi cento numeri (in pratica il centesimo numero triangolare). E Gauss che fa? Dopo due minuti se ne torna con la soluzione (5050) lasciando il povero insegnante esterrefatto. Cone fece Gauss? Semplicemente associò alla sequenza crescente 1,2,3,4…100 la stessa sequenza, questa volta decrescente, sommandone i termini corrispondenti (1 con 100, 2 con 99, 3 con 98…) Provare per credere: ogni somma fa 101. Il 101 preso 100 volte fa 10100. Ma le sequenze sono due, quindi dividendo per 2…. fa 5050!
Non voglio tediare te e i tuoi ospiti, ma adesso arriva la magia. Pare che oltre a Gauss, già i Pitagorici avessero individuato la formula per la somma dei primi n numeri naturali: n x (n+1) /2
Ma quanto fa 1+2+3+4+5+6+…. fino all’infinito?
In effetti la somma (serie per gli addetti ai lavori) è divergente e la risposta corretta è infinito.
Per tutti era infinito, tranne che per uno dei più affascinanti geni della matematica mai esistiti: Srinivasa Ramanujan (1887-1920).
Indiano, di classe povera, autodidatta, nel 1913 mandò una lettera al Prof. Hardy del Trinity College di Cambridge, piena di formule a dir poco geniali. Tra queste la magia: la somma infinita dei numeri naturali, dice Ramanujan, fa -1/12 (proprio così “meno un dodicesimo”!). Uno dei risultati più emozionanti e misteriosi della matematica. La storia continua ed è romanzata nel libro e nel film “L’uomo che vide l’infinito”. Sta di fatto che, con certe premesse e sotto certe ipotesi, quel risultato è stato dimostrato ed utilizzato in fisica quantistica e funziona straordinariamente bene (teoria delle stringhe, vuoto quantistico etc.).
Magia come promesso per chi ha resistito: …dal triangolo all’infinito…
Quando, Emanuela, parli di Arte e Matematica io sono assolutamente con te: ai livelli più alti queste due dimensioni coincidono e rilasciano emozioni indescrivibili difficilmente esprimibili a parole.
Ho poco da commentare. Solo una gradissimo GRAZIE!
A proposito di Munari: “La nascita del triangolo”
muchas Gracias, me ayudo mucho 😀
Molto bello “IL TRIANGOLO” di Bruno Munari, ed. CORRAINI, dello stesso autore anche “ILQUADRATO” e”IL CERCHIO”.
Complimenti per i contenuti di questo blog.
Sì, Munari è un vero Maestro! 😀
Un articolo molto interessante, per imparare con gli alunni per conoscere differenti funzioni del triangolo.. Una buona forma di suscitare la loro attenzione, con esempi di opere d’arte degli artisti diversi, anche attraversare e conoscere un po diversi momenti storici. Grazie!!!
Grazie a te Valeria!
Valido metodo per veicolare in modo interdisciplinare contenuti che condivido.
🙂
SONO SEMPRE INTERESSATO AI VOSTRI POST. COMPLIMENTI
Grazie mille! Continua a seguirmi 😉